Solved Problems
Introduction
I want to showcase some cool problems that I have solved in the past couple of years. The problems below are special to me. I found them interesting to reason with and difficult, but I am glad I got the opportunity to learn by completing them.
Ellipse Twins
This is a genius problem and one of my favourites. It has many small details that you have to pay attention to, and it tests a lot of knowledge.
I am really proud of my solution to part D.
I first found the area by hand using polar integration, and then setup the integral in cartesian coordinates and used a CAS to evaluate it. The results matched up and it was super satisfying.
Furthermore, when I was solving the integral in part D, I encountered something new. When I was blindly plugging in the bounds to complete the integral, I kept getting the wrong answer. It turned out a subtle singularity was occuring between the lower and upper limits, and so special care needed to be taken when plugging in the bounds.
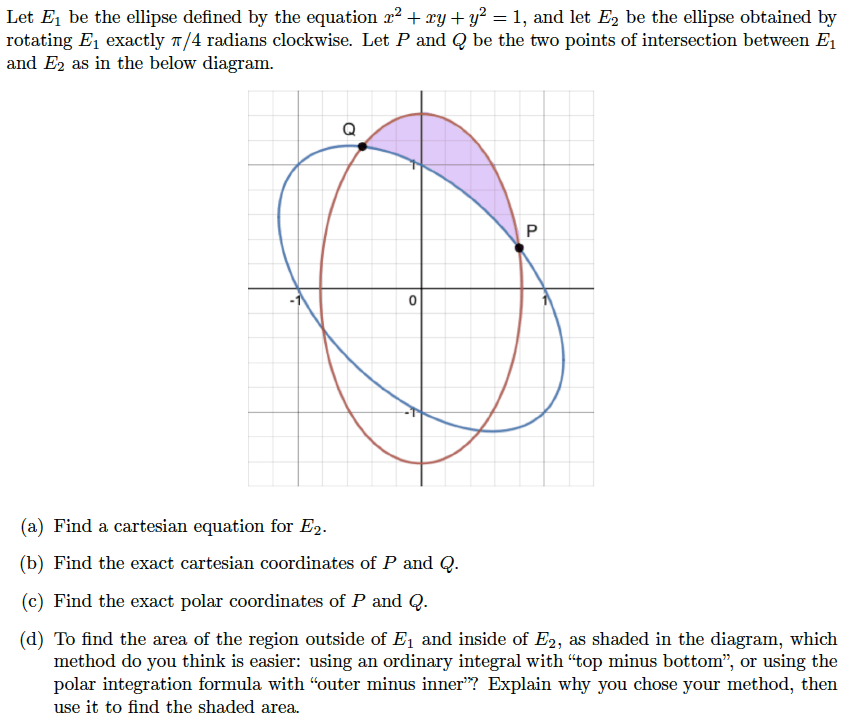
Credit: Professor Ehsaan Hossain. MAT232 Multivariable Calculus.
A Golden Intersection
I am really proud of my solution to this problem; it explains the steps clearly and contains many nice images to guide the reader.

Credit: Professor Ehsaan Hossain. MAT232 Multivariable Calculus.
Murder Mystery
This problem is super unique and one that I will never forget—probably because it was a nightmare for me to figure out. The solution isn’t too complicated; the complicated part is deciphering and picturing the problem.
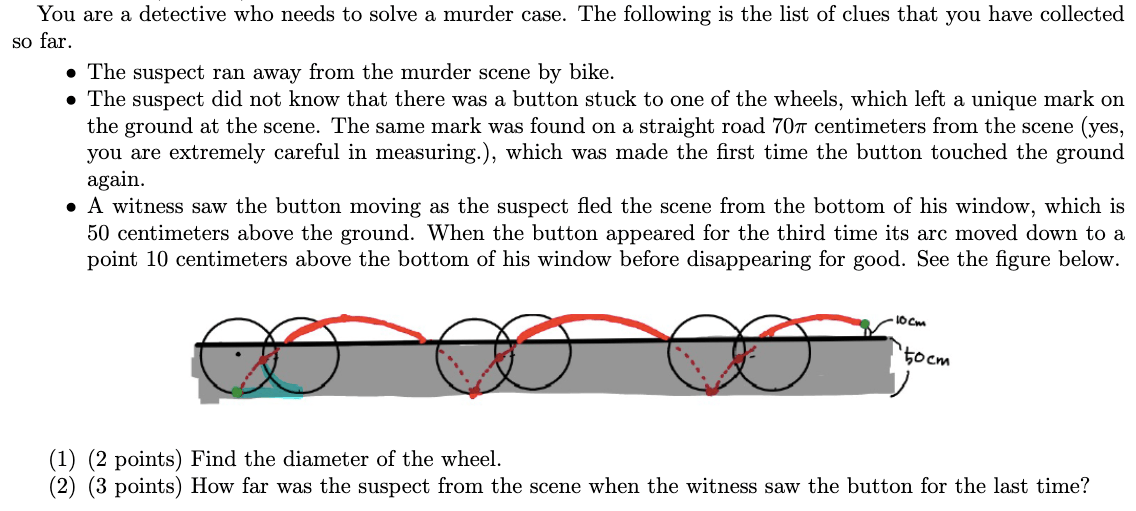
Credit: Professor Mike Pawliuk. CC BY-NC-SA 2.5 Canada.
Lifetime Supply of Cookies (100% Legit, Not a Scam)
Here’s a fun problem in which we need to come up with a strategy to always win the lifetime supply of cookies.
I believe this problem is supposed to whet our appetites (pun intended) for solving games within the broader field of Game Theory. A solved game is one in which the outcome can be predicted from any position. In our case, we are trying to strongly solve this cookie game.
Did you know that connect 4 and tic-tac-toe are also strongly solved? Meaning that there is an algorithm that you can follow to always guarantee a win (or at the very least, a tie).

Credit: Professor Michael Miljanovic. CSC236 Introduction to the Theory of Computation.
Space Voyager 3021
Here is a fun multivariable calculus problem where we need to find the volume and surface area of the space voyager.
This is the longest solution to a problem I have ever typed on LaTeX!

Credit: Professor Ehsaan Hossain. MAT232 Multivariable Calculus.
Range++
Credit: Professor Shay Fuchs. MAT102 Introduction to Mathematical Proofs.
I was familiar with the concept of the range of a function since high school. In this question we need to prove that the range is a certain set—which can be much harder. This question does not seem as interesting as the others, but this question is special to me. When I was in first-year I could not wrap my head around problems like these no matter what I tried. However, now a problem like this is no issue to me—which shows my mathematical development.
Full House
Here is a problem related to combinatorics. I find combinatorics tough, and so I am proud of getting this problem correct on my first try. This problem requires case work and attention to little details.

Credit: Professor Timothy Yusun. MAT202 Discrete Mathematics.
Linear Bijection
Here is a nice linear algebra problem with a clean solution. We need to show that the given transformation is a linear bijection (in other words, an isomorphism). The solution can be shortened a bit by noticing that the transformation is a linear operator.

Credit: Professor Mike Pawliuk. MAT224 Linear Algebra II.
Closest Points
There are many methods to find the minimum distance between two lines, however, when we also need to find the point on each line that results in that minimum distance, we can use Linear Algebra to help us.



